Concepts

This is an excerpt from the book series Philosophy for Heroes: Knowledge.

If names are correct, there is order; if names are allowed to become confused, there is disorder. What causes the confusions of names are explanations that involve an excess of elegance and subtlety. If explanations involve such excesses, then the not-acceptable is called the acceptable, the not-so is called so, the incorrect is called correct, and the not-wrong is called wrong. —Lü Buwei, The Annals of Lü Buwei

Now we know how our process of perception works. But we are not an infinite video recorder which saves all perceptions one after the other. In addition, the universe itself is potentially infinite (or at least very large). But our consciousness possesses an identity and, for this reason, is finite. How can we then grasp a potential infinite amount of information with our finite mind?

A solution to this problem is concepts. Concepts are abstractions that permit us a description of reality and allow us to form compact units of information from many different origins, which can then be processed by our short-term memory. For our further progress, we first consider a list of fundamental concepts as a kind of reference basis. Figure 1.3 and Figure 1.4 illustrate an overview of, and context for, the concepts listed below. Here we see, in particular, the interdependencies governing them.

CATEGORY ·  A category is the mental correlation between entities.

CONCEPT ·  A concept is a category that is delineated by a definition, and determined by the nature of the entity.

‍

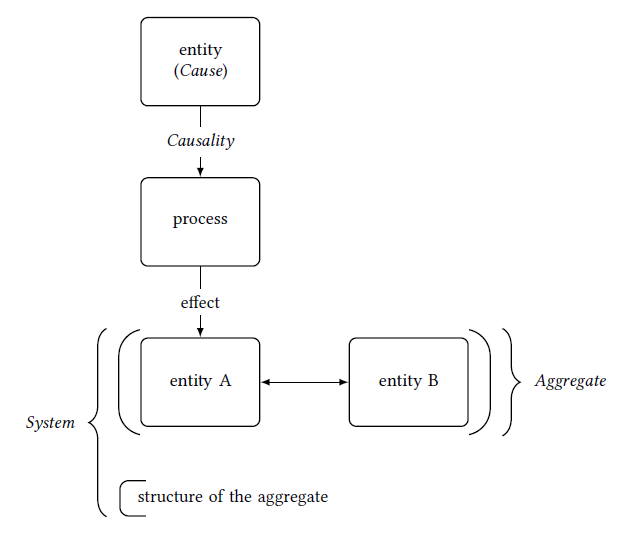
CAUSE ·  A cause refers to the entity that has or had an effect on another entity (e.g., the ice cube in the glass is the cause for the drink having gotten cold).

CAUSALITY ·  Causality refers to the effect of one or several entities on another entity in a certain situation (e.g., an accident is no random occurrence, there are one or several causes which led to the accident, such as lack of sleep, a technical defect, poor visibility, etc.).

AGGREGATE ·  An aggregate is a number of entities that have a reciprocal effect on one another, so that they can be considered collectively as their own entity (e.g., a cup full of water—all water molecules interact with each other).

STRUCTURE ·  A structure is a description of required properties, dependencies, and arrangement of a number of entities (e.g., cube-shaped).

SYSTEM ·  A system is an aggregate with a definite structure (e.g., an ice cube is a system of frozen water molecules).

POINTER ·  A pointer can be a word, picture, gesture, etc. that “points” to one or more entities. It can be used in their place, e.g., if you “point” to a specific apple by saying “this apple,” you do not have to actually take the apple in your hand to make it clear about which apple you are speaking.

TERM ·  A term is the name of a concept (e.g., as a word or fixed word combination, such as “goods and services” or “in a jiffy”). Every concept has a term pointing to it, but not every term is a concept (e.g., conjunctions like “and”).

DEFINITION ·  A definition is the possible demarcation of a number of entities by means of perceptions, concepts, and axioms (e.g., grass is a “plant,” a “living organism” which uses “photosynthesis.”) It consists of a list of properties and processes of entities in question.

‍INTEGRATION ·  Integration is the classification of perceived entities into one or several concepts, as well as classification of existing concepts into more general concepts or a concept hierarchy (e.g., the classification of a perceived sound wave as a definite word, or classification of the concept “human” into the more general concept “life-form”).

CONTRADICTION ·  A contradiction can result from a (possibly erroneous) logical integration. This becomes visible when the corresponding concept has a property while not having it at the same time (such as an invisible pink unicorn, boiling ice, a full empty cup, etc.).

LOGIC ·  Logic is the method of non-contradictory integration of knowledge or perceptions.

KNOWLEDGE ·  Knowledge constitutes sense data, logically integrated perceptions, concepts, or concept hierarchies. It can also be created from logically integrated conclusions from existing knowledge.

Biography —Aristotle Aristotle lived around 384 to 322 BC in ancient Greece and was a naturalist and philosopher. He is considered the founder of Western philosophy and sciences and a proponent of this world, our reality. Though a pupil of Plato, he discarded Plato’s theory of forms; instead, he propagated the view that reality consists only of entities that can be perceived, and that concepts, thoughts, and imaginations themselves have no properties and do not exist on their own. According to Aristotle, entities act according to their nature and the world is not a shadow of a “divine dimension.” It exists on its own—perceivable and intelligible by the human mind.

Concept Formation

Why is it necessary for concepts to be based upon observations, but not measurements?

When faced with new perceptions, we might have to form new concepts and definitions. As described previously, a concept involves a mental connection of entities, which is described by a definition and determined by the common nature of the entities. So we consider not just the effect of a single entity through measurements, but instead abstract and connect sense data perceived from an entire series of entities. This abstraction is achieved by enumerating only the common properties of the entities and omitting the measurements of the entities. For instance, we observe blue, yellow, and red ball-shaped entities. Instead of creating separate concepts for each color, we form the concept “ball” with the property “color.” The configurations of the property—the colors blue, yellow, and red—no longer appear in the definition of the concept. Basically, this corresponds to the aforementioned reflection of our individual experiences of our consciousness (qualia).

Concepts are generated through the omission of measurements.

Example When we have selected our concepts properly, we do not have to adapt them even when making surprising new discoveries. A famous example pertains to swans. Just because we have only seen white swans does not necessarily mean that “whiteness” is a substantial property of the definition of a swan. Color is a property, black and white feathers constitute a measurement. If we find a black swan, we can reuse the concept of a swan, using black instead of white for the property of color.

How do concepts increase our mental capacity?

Our new knowledge of concepts can also be applied in reverse. Assuming we have defined our concepts properly, we know that two balls of different colors will roll the same way down a slanted surface. Rolling is a behavior related to its shape, not color. So instead of having to run two separate experiments and to describe the process of rolling for each individual color, we can predict the behavior for a ball of any color with the definition of a single concept.

With the aid of concepts, we can make statements about the behavior of a large number of entities without having to consider them individually. This way, we increase our mental capacities multifold.

Establishment of a Definition

“See how bad a story you can write. See how dull you can be. Go ahead. That would be fun and interesting. I will give you ten dollars if you can write something thoroughly dull from beginning to end!” And of course, no one can. —Brenda Ueland, If You Want to Write: A Book about Art, Independence and Spirit [Ueland, 2012, p. 65]

Definitions do not need to be complete; what is their role?

Concepts always encompass all properties of the entities, regardless of which definition we give them at the moment. In contrast, for a definition, not all properties must necessarily be specified. We do not have to be omniscient to provide a proper definition. In the majority of cases, definitions are incomplete. But at a minimum, definitions should differentiate their associated concepts from other similar concepts. The reason for an incomplete definition could be that we simply have not yet discovered all properties of a concept. Without the presence of another concept that overlaps with the definition of our concept, a complete definition is not necessary. [cf. Rand et al., 1990, p. 99]

Definitions do not need to be complete; they simply must be able to clearly separate concepts from one another.

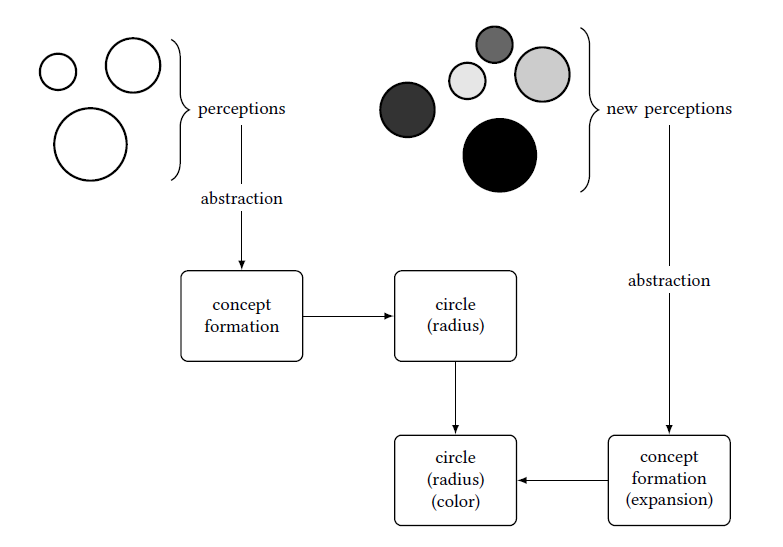
Figure 1.5 shows the perception of three circles of different sizes, from which we define the concept “circle” with the property “radius.” As long as we have seen only gray circles, the definition of “circle” and “gray circle” would be identical. If we make subsequent perceptions of circles of different colors, we can then add the property of color. With our initially limited perceptions, the original definition was correct, in the sense that it correctly encompassed all existing perceptions. With subsequent perceptions, it was necessary to broaden our definition of the existing concept and add the color property.

‍

Not every concept, however, is suited to help with the comprehension of the world. For example, there are concepts with contradictory properties (“round rectangle”), concepts which represent enumerations (“all horses and pigs”), and concepts which depend directly on the results of measurements (“blue horses”). Ultimately, just because we can write down a definition of a concept, this does not mean that it is necessarily a valid concept.

I want to emphasize here that concepts do not, as Plato believed, “inhere” in an entity. Thus, no “person-concept” resides within a person. Concepts themselves are not entities or properties. Instead, they are pointers to categories. They concern purely mental constructs, with whose help we try to abstract and simplify nature to the point that we can apply them productively. They thus depend on our situation, our knowledge of the world, and our needs. To what extent they help us in life naturally depends on the degree to which they are free of contradictions in their construction, whether we have correctly integrated our perceptions, and whether we have made sensible decisions in separating the concepts from one another.

Grenzerfahrung ·  Grenzerfahrung is German and literally means “boundary experience,” an experience that tests our abilities and ideas to the limit.

In summary, we can say that learning new concepts happens best when we become aware of their boundaries. In general language usage, this is designated “expanding one’s horizons,” or simply constantly trying out new things. If we push ourselves to the limit and make so-called Grenzerfahrungen, even negative experiences themselves can help us to define and perceive the positive more sharply. If we have never experienced failure, we do not know our own boundaries, which ultimately diminishes either our self-esteem or our well-being.

Concept Hierarchies

How are contradictions in statements related to concepts?

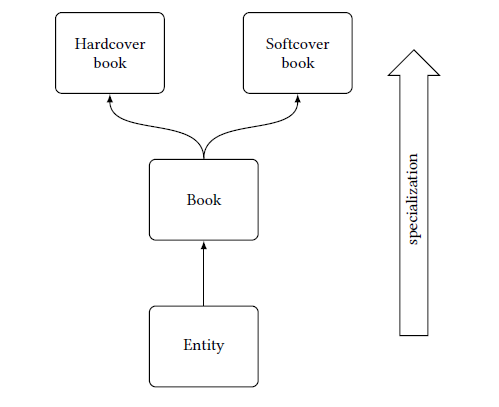
First having found individual concepts, we can then use these concepts as the basis for new, specialized concepts. Hence, we need not consider each situation separately. If we apply these dependencies of specialized to more general concepts, a type of tree structure arises—a concept hierarchy. Each branch constitutes a general concept, and each leaf constitutes a more specialized concept.

The trunk (the “root”) constitutes the most general (“entity”) and a leaf a specialized concept (e.g., “softcover book”) of the corresponding concept hierarchy (see Figure 1.6). In this model, a concept lying further out inherits the properties of the more general concept. For example, “table” is a specialization of “furniture.” For this reason, the higher-level concept always encompasses (“inherits”) all entities of the more specialized concept, while the specialized concept encompasses only a portion of the entities of the higher-level concept. This strict dependency and succession of the concepts are of great importance and a necessary prerequisite for our work with concepts. [cf. Rand et al., 1990, pp. 43,106] The hierarchy permits us to learn many different concepts without having to re-comprehend and describe the world from the ground up each time.

‍

CONCEPT HIERARCHY ·  A concept hierarchy is a tree-like structure consisting of concepts, defined by the definitions of given connections (e.g., “chair” and “table” are furniture, the concept “furniture” would thus constitute the root of a tree and “chair” and “table” are two successive branches).

INHERITANCE (OF A CONCEPT) ·  A concept with an inheritance of another concept builds upon the other concept’s definition. If the concept “table” inherits from the concept “matter,” the former would build upon the property “mass” of the latter.

HIERARCHY TREE (OF CONCEPTS) ·  A hierarchy tree of concepts refers to the directional ordering of concepts according to their inheritance.

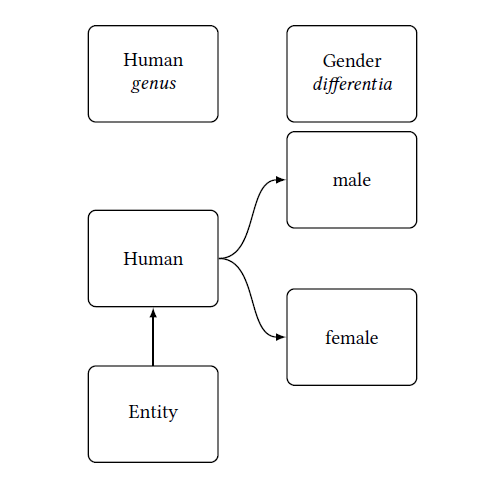
In philosophy, this kind of structure of concepts is called the genus proximum et differentia specifica and traces its origins as far back as Aristotle. It consists of a genus—the overarching, more general concept—and a differentia—an attribute by means of which we can differentiate the concept from other concepts. In the case of “a female human,” “female” (the gender) is the differentia(“female” categorizes humans into women and “non-women”) and “human” is the genus (see Figure 1.7).

‍

To conclude, it should be noted that with the aid of theoretical knowledge about concepts, we can also examine our own concept hierarchy in our mind. This can be done by systematically considering each concept, level by level, and checking for contradictions. Should we stumble upon (apparent) contradictions in the course of using concepts, there must be either a classification of an entity under the wrong concept, or a faulty definition of that concept.

The origin of contradictions lies either in the faulty definition of concepts or in the faulty allocation of entities to concepts.

Conceptual Common Denominator

Sometimes it can indeed be practical to loosen this strictly tree-like structure a bit. To illustrate, the concept “mammal” applies to humans just as well as the concept “biped” does, although “mammal” and “biped” are almost independent concepts, coinciding only on a completely abstract level in the hierarchy tree (e.g., “bipeds” and “mammals” represent matter which moves by itself). We could now either define both concepts twice (“two-legged mammals”, “four-legged mammals,” “mammals,” “bipeds,” and “quadrupeds”), or we just define them individually and allow combinations of concepts. The first alternative is shown in Figure 1.8 on the left, the second one, with the so-called conceptual common denominator, on the right.

CONCEPTUAL COMMON DENOMINATOR ·  If a concept inherits from more than one other concept, these additional concepts will be called conceptual common denominators. For example, we can classify a “human” entity into the concept “mammal” just as well as the concept “biped.”

‍

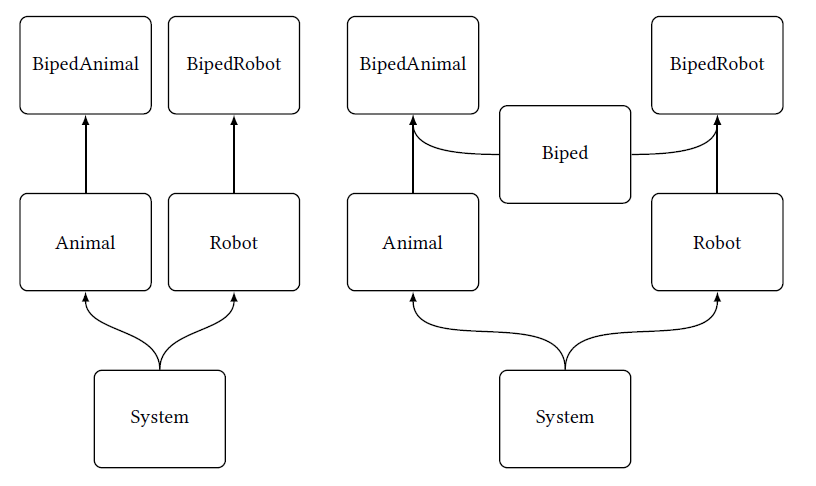
The right-hand illustration in Figure 1.8 allows us to abstract a property already understood and use it again for a multitude of concepts. For instance, we can expect that a two-legged robot climbing stairs will have to overcome similar challenges as those faced by a human climbing stairs. Likewise, while sharks and dolphins are both sea animals, they merely represent very distant biological relatives. But owing to their similar living conditions, we will presumably find correspondingly similar properties in areas such as body shape, movement, or skin. A conceptual common denominator such as “sea organism” could thus help us better understand the world of sea animals, as we can re-apply insights about properties such as the streamlined body shape to a whole variety of animals without having to repeatedly examine each individually.

With conceptual common denominators, we must take care that there is no overlap of properties. An “ape-like horse” may ascribe typical character properties of an ape to a horse but, due to the multitude of overlapping properties between the concepts “horse” and “ape,” this is difficult to determine solely by means of the expression. [cf. Rand et al., 1990, pp. 41–42]

Boundary Cases

The opposite of the aforementioned Grenzerfahrungen are boundary cases, when we are not trying to explore the extremes of a concept, but instead cannot decide whether an entity belongs to one concept or another. To illustrate, imagine a line on the floor; we throw a number of dice into the vicinity of the line and establish two concepts: “left die” and “right die.” As a definition, we stipulate that a die touching the line belongs to the side containing the larger part of it. With this setup—even with the best measuring techniques—undecidable cases can occur. Does this mean that our method of establishing the concept was faulty and that we need a third concept for such a borderline case? Would there not also be a need for other borderline cases, thus leading to the collapse of our complete system of reasoning for concepts?

Example In philosophy, this problem is known as “sorites,” or the “sorites paradox”: “When is a mound of sand a mound of sand?” or “How long does a mound of sand remain as such if we remove individual grains?” With this, people try to suggest that we could not really perceive the world by means of concepts and that we would have to live always with a “fuzziness” in our knowledge.

But actually, there is an answer to this “paradox.” It becomes clear if we step back for a moment and remember the definition of concepts. An essential part was the omission of measurements. So, whenever we can achieve the classification of an entity into a certain concept only through a measurement, we have to re-examine our concept hierarchy. We have to unify all concepts that are dependent on a certain measurement into an overriding concept. Next, for the definition of this new, more general, concept, we discard the measurement and replace it with a property.

The general idea is that we should proceed economically and keep the number of concepts as big as necessary but as small as possible. If we face concepts like “small table” and “large table” and have difficulties categorizing a “medium-sized table” in one of these concepts, we create a more general concept “table” and add the size of the table, as a property, to the definition. Simply put: a table is a table, whether it is located at the moment in a house or a garden, and whether it is blue or green, small or large. [cf. Rand et al., 1990, pp. 101–4]

With the example of the dice and line, measurements are necessary, concepts of the type “left die” and “right die” thus cannot exist. Instead, a “die” would have a property “position,” whose value we measure or set in relation to something else. In the example of the mound of sand, the error lies in a somewhat different place. If we answer the question about the mound of sand with “Define mound of sand!” then the dance around the question begins, since the questioner does not want to concede for the purposes of the argument that mounds of sand consist of a number of grains of sand, and single grains of sand also constitute a number. This behavior usually marks the point in our discussion at which the opposite side begins to cast doubt on the objectivity of language.

The origin of such imprecise concepts lies with Plato. He argued that there had to be a third truth value. Questions like: “What is the difference between an amount of sand and a mound of sand?”, “How many grains of sand does it take to constitute a mound of sand?”, or “Is a single grain of sand a mound of sand?” imply that there was a third logical condition besides “true” and “false,” hence it is called the “argument of the law of excluded middle.”

This type of argumentation is often used as an attack on concept formation. First, a concept is erroneously connected with a measurement (“Mounds of sand consist of at least three grains of sand”), then the absurdity of such a definition is pointed out, and finally it is declared that you cannot define concepts because of that. This ultimately leads to a situation where we no longer can make any clear statements about the world, particularly about truth values. This is a fallacy of the stolen concept. Whenever we encounter an argument like this, we should discuss the underlying concept and the incorporated measurements, and not be fooled into arguing about the boundaries of the imprecisely defined concept.

Concepts in Computers

I propose to consider the question, “Can machines think?” —Alan Turing, Computing Machinery and Intelligence [Turing, 1950]

How do humans and computers compare in terms of comprehending an actual issue?

With a thorough, theoretical understanding of concepts, we can also easily pass on this structure of knowledge to other conscious entities. By this, we obviously mean first and foremost the consciousness of other humans, but we also see advances being made, especially in communication with other life forms. While we could never conceivably communicate with, for example, dolphins in the human sense, our knowledge of concepts can at least classify which stage of development other animals have reached in comparison to humans. Other than humans and animals, in the last century there has arisen a completely new domain of application: the computer.

A computer is something like an industrious worker who can take out, read, describe, and compare file cards from a large file catalog. Though it may require a great number of file cards, in principle, such a computer can solve any problem, be it coordinating a global network, deciphering the human genome, or designing a modern automobile. This basic model of a computer is called a “Turing machine,” invented by Alan Turing in 1936.

Biography —Alan Turing Alan Turing (1912 – 1954) was a British pioneering computer scientist, mathematician, logician, cryptanalyst and theoretical biologist. He was highly influential in the development of computer science. Turing is widely considered to be the father of theoretical computer science, artificial intelligence, and evolutionary computation. He is one of the many silent heroes that contributed to winning the Second World War against Nazi-Germany by cracking their “Enigma” code, an encryption protocol that was used for military communication. Tragically, after the war, he became a victim of prejudice against homosexuality.

Some readers might remember a time when searching for a book meant visiting an actual library, and opening an index-card cabinet with alphabetically sorted cards, one for each book. On each card, there was the book’s full name, author, category, and location in the library. With that information, you could easily find the book in question on the shelves. You can imagine that each card is like an abstracted entity based on the definition of the concept of a book in a library. This kind of index system describes the situation of the available books in the library very well.

Actually, we can expand such an index-card system to describe any situation. We just need to add additional types of file cards and the possibility for a file card to reference another card. This is exactly what we have discussed earlier in terms of a concept hierarchy, definitions, and entities. The difference compared to a computer is that a computer processes those file cards digitally and much more quickly than a human can. Thus, a modern computer can “understand” any situation it is programmed to and “think” conceptually in a similar way as we do. To describe the concept hierarchy in a computer, we use so-called object-oriented programming languages. With their aid, we can efficiently depict any real situation on a computer. By “efficiently,” we mean that we can refer to existing parts of programs (existing concepts) in new situations—just as we ourselves use already known concepts to understand new situations.

A computer is like a large stack of indexed file cards in which a programmer can represent a concept hierarchy similar to our own in a structured way. Both computers and humans use concept hierarchies to categorize elements of a situation.

Did you know? The knowledge behind concept hierarchies can be programmed into a computer with the help of a programmer. Programming a computer to create concepts on its own (using its sense data) is much more difficult, though. For this, we need an understanding of induction and deduction. With a better understanding of philosophy and human creativity, science is steadily making progress to create a computer program whose behavior resembles human intelligence. But will it also be self-aware? Read more in Philosophy for Heroes: Act.

Let us consider this tangibly by reference to the example of a pizza delivery company. There, orders, inquiries, customers, and employees must be managed. The first step of management is an accurate grasp of the current situation. Instead of verbally surveying each employee and customer and placing a summary in a file, we abstract the properties of the relationship to each respective person. The employees may have much to tell about their lives, but only a few items of data are important for the payment of their wages, such as a name and bank account number. The same holds for the client, for whom we actually require only a delivery address. In addition, we must manage our products (the pizzas) and the individual inquiries and orders. Just as in the construction of our concept hierarchy, here also we try to determine the properties of an entity and disregard all other information.

‍

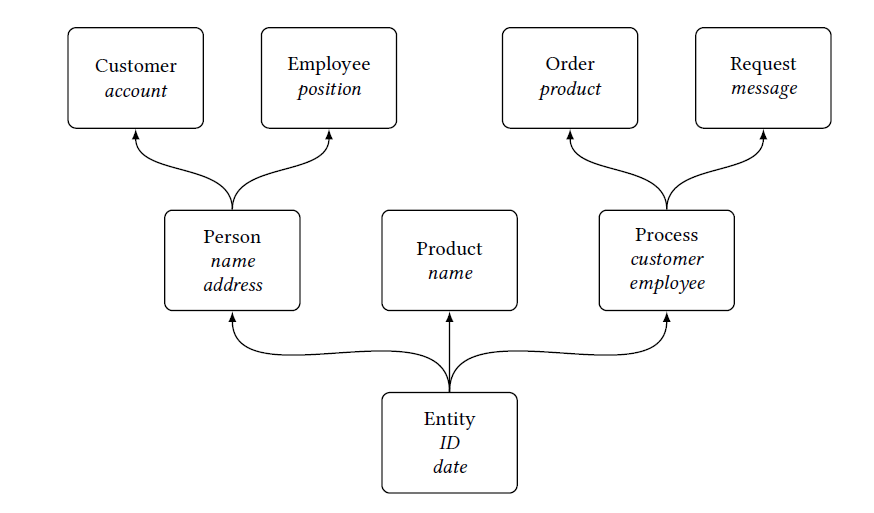
As all the parts of our company designated above should at the same time refer to identifiable entities with a creation date, they should inherit from a more general concept named “entity.” And obviously, “clients” and “employees” are persons; we can thus let properties such as the address inherit from a more general concept, “person.” With the definition of “order” and “request,” we must in both cases reference the person placing the order (customer) and the employee processing the order (employee), and thus generalize the properties in a concept called “process.” Let us supplement these definitions with properties of the customer (his account), the employee (his position in the company), the order (the ordered product), and the request (the customer’s message); we now obtain a schematic construction of this small slice of the world as in Figure 1.9.

Example A further example for a common problem that we can solve with a computer with the help of concept hierarchies would be the ordering of a plane ticket. For each passenger, this proceeds according to a very similar model: the flight plan, flight conditions, seat assignment, and personal data, among other things, must be managed and monitored. Without these essential concepts, we would have to require every single passenger to write a summary of how she envisions her trip. Different people might like to spend the trip watching a movie, be served a hearty lunch on a short domestic flight, or postpone the flight by a half hour. Organizing a flight with more than one hundred people while observing all of these special, possibly conflicting, requests would be very time-consuming, if not impossible, without using a concept hierarchy.